
Mercedes surprised no one by regularly topping the timing screens in Formula 1 testing at the start of this year. They did, however, manage to spring a surprise when one of the enabling innovations was revealed: DAS or, to give it its full name, dual-axis steering.
On-board footage showed both Lewis Hamilton and Valtteri Bottas pulling the wheel towards them on the straights, before pushing it away when reaching the corners. They could not hide it any longer, and technical boss James Allison was seemingly happy to confirm its existence – if very little about what it was actually doing.
The innovation, it later transpired, was all about dynamically altering the toe-angle of the front wheels of the car.
Why would Mercedes want to do this? To briefly explain, toe is the angle that the wheels sit in relation to dead ahead when the steering is straight. If the front of the wheels are pointing out, this is known as toe out, the opposite and they are toed in.
The toe angle has a significant effect on a car’s handling and changes how the tyre interacts with the road surface. Generally, a degree of toe out will aid both stability and grip on initial turn-in to a corner, however, too much toe out means the tyre scrubs – effectively it is dragged rather than rolled across the track surface.
TRIZ-wise, here’s a classic physical contradiction: the car wants toe-out and it doesn’t want it. Something like this:
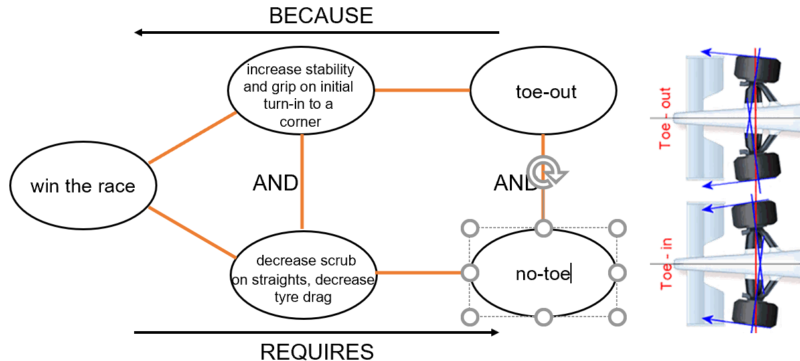
Once we know there’s a contradiction to be solved, all we need to do is think about the three different separation strategies and we’re half way to a solution. Actually, in this case, all we need to do is think about the first of these strategies, separate in space. Where do we want toe-out? Where do we not want it? As soon as we realise the two questions have a different answer – corners versus straights – we can start tapping in to the solution strategies of others. The most common of which is Principle 1, Segmentation.

Simple when you know how. As ever, the real trick is giving yourself permission to believe that contradictions don’t have to be solved by the usual trade-off strategies.
