Imagine an archer facing a wall 10 metres away and about to fire lots of arrows at it. The archer is not so accurate and will shoot randomly within a plus or minus 45-degree angle as shown in the figure:

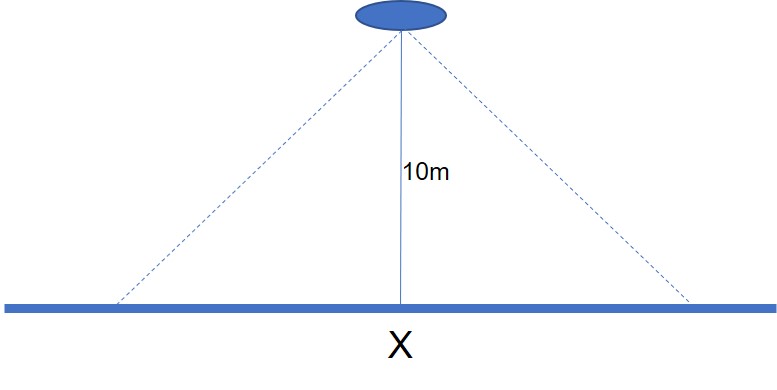
The question is, if X is the point on the wall directly perpendicular to where the archer is standing, when lots and lots of arrows have been fired, what’s the average position along the wall that they will end up?

The answer is, of course, that X marks the average.

Now let’s rotate the archer by 45-degrees and, retaining the same plus or minus 45-degrees random accuracy range, what will be the average position on the wall after firing lots and lots of arrows this time?

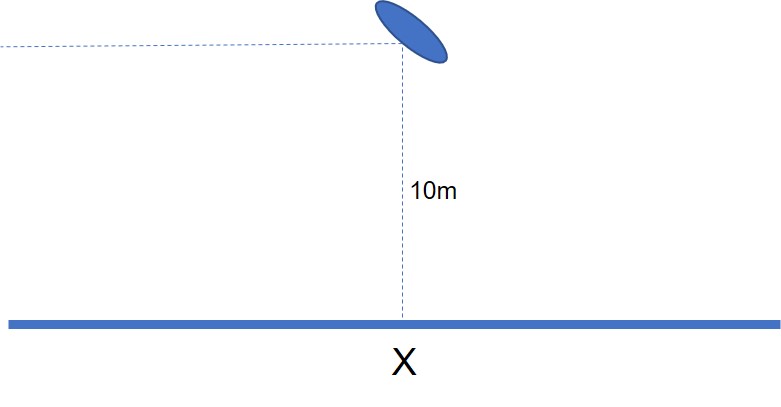
This calculation is a little bit more difficult unless you can remember some of your school-level trigonometry class work on right angled-triangles and tangents being opposite over adjacent.

Most people’s instincts let them down when trying to answer this question.
What are your instincts telling you right now?
If you had to answer the question, what would you say?

I went to a Twitter-sparked AntiFragile meeting yesterday and Mark Baker (aka the rather famous @guruanaerobic) showed everyone a lovely sequence of YouTube videos of a father talking his son’s through the problem. If you’ve ever got 20 minutes to spare, you should watch them (https://mikesmathpage.wordpress.com/2018/04/08/sharing-an-advanced-expected-value-problem-from-nassim-taleb-with-kids/).

It offers an inspiring journey involving a computer programme that allowed the kids to fire millions of random arrows at the wall and see what the average distance from X turns out to be. The main learning being that their (and I think most people’s) instincts are quite badly mis-calibrated.

The answer, in case you’re interested, is infinity.

Most people can’t imagine this could be the case. That’s because most situations we encounter in life are like the first, symmetrical version of the problem. In this version, the arrows all hit the wall and thanks to the symmetry are equally likely to end up one side or other of the X point. Which then means that, the more random arrows we fire the more likely everything balances out to make X the average. This problem is convergent.

In the second case, however, not only is there an asymmetry, but there is also the possibility that a fired arrow might end up being fired exactly parallel to the wall, in which case it will never hit the wall. This second problem contains a non-linearity. Remote as the extreme possibility might be (it is, after all, right at the limits of the range of randomness of the archer), it is nevertheless a finite possibility. The more arrows the archer randomly fires, the more likely this remote possibility comes true.

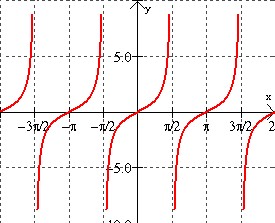
Anyone that can remember those trigonometry lessons will have a vague recollection that the tangent graph contains exponential characteristics. And whenever we see such a phenomenon – they’re everywhere in the real-world (for example in s-curves) – we know that our human instinct for linearity is no longer a good idea.

The father-son videos offer up an inspiring illustration of kids re-thinking their instincts. The magic in the videos comes from the way dad gets his sons to hypothesise their answers and then runs increasingly more simulations to test them. It’s great learning.

One of the points I tried to make during my 20 minute ‘this is what antifragile means to me’ post-lunch diatribe was that the aerospace industry is the safest industry on the planet because it has learned to be more antifragile than other industries. Accepting the non-linearity of the world, like what dawned on the kids in the video, was an early stage in this journey.

Later on, you begin to realise that running millions of trials to test your non-linear hypotheses is a very expensive business. I once destroyed a jet engine on test. The rate of spend during the failure was around £2M per second in today’s money. Spending like that makes you quickly recognise you have a contradiction – you want to continue to be the safest industry on the planet but you also need to innovate and try new things without spending all your money exploding thousands of expensive engines. The way you solve this contradiction is you work out what the worst case is, then add a big safety margin, and then design for that. You quickly learn that you don’t learn anything from doing millions and millions of ‘average’ things. Averages are pretty much meaningless in complex, non-linear worlds.

An aerospace engineer tasked with working out the second archer problem has retrained their instincts to not need millions of trials to know the answer is infinity. You only need to run one trial: the extreme one. The worst case in the second archer problem is that the arrow flies parallel to the wall and thus never hits the wall. The extreme X answer is therefore infinity. Calculating the ‘average’ is then going to be done by summing all of the distances from x from each random arrow, then dividing by the number of arrows fired.. When the extreme case happens the number of arrows fired will have been finite, the average is going to be infinity-divided-by-a-finite-number. Which equals infinity.

Retraining our linearity-assuming brains to acknowledge non-linearity is hard. Even though the kids in the video learned something important, they’d need to see a bunch more examples of non-linearity to really get the point. The point is the journey. Retraining our (first principle-holding) brains to shift away from averages to extremes, however, is somewhat easier. It’s also a good step in the antifragile direction. One smart (extreme antifragile) trial always beats a billion dumb (random/average) ones.